Research
Our primary research interests are in the timing variability of accreting black holes and neutron stars using data from instruments onboard satellites such as the Rossi X-ray Timing Explorer, Swift, Kepler, and TESS in combination with ground-based optical observatories for spectroscopic follow-up. We are also currently developing methods that accommodate unevenly sampled time series to study optical timing data from the Zwicky Transient Facility of unique compact binary systems in preparation for the era of big data astronomy with the Rubin Observatory Legacy Survey of Spac and Time (LSST). The goal is to understand the fundamentals of accretion physics and how various aspects of the accretion flow modulate emission over time. We employ methods from nonlinear dynamics and chaos theory for comparison to traditional Fourier-based techniques and Bayesian statistics as a means to create a new and complementary classification of transient and variable astrophysical systems. Side projects include developing radiation-hydrodynamic simulations of the accretion disks around black holes and exploring interdisciplinary applications of novel time series analysis methods.
Plenary Talk at the Transient and Variable Universe conference in June 2023
“Novel Metrics for Time Series Analysis of Accreting Systems”
Held at the University of Illinois, Urbana-Champaign
Accretion on to Compact Objects
One of the most common mechanisms for power generation in the cosmos, besides the nuclear fusion that powers stars like our Sun, occurs through the accretion of matter onto a massive object. Accretion of matter onto a simple point source with mass is essentially the conversion of gravitational potential energy into kinetic energy. Nuclear fusion in the center of the Sun produces about one twentieth of the power as that from accretion onto a neutron star with comparable mass to our Sun. The impressive power generated through accretion comes from the large ratio of the mass of the central object to its radius. The more compact the object, the more that accretion will dominate as the power source. There are many observations of point sources in the night sky for which a massive amount of luminosity is generated within a small radius, which can often only be explained by accretion onto a very compact object such as a black hole or neutron star.
Accretion can take place through various geometrical means. The simplest example is spherical accretion where a single point source, such as a star, is embedded inside a homogeneous gaseous cloud or background medium. The surrounding medium will begin to fall radially inward, due to gravity, onto the central star. If we were to then consider gas that has some intrinsic angular momentum, then the embedding material will seek the preferential geometry of a disk aligned with the orbital plane. Binary systems are the most common example in the study of these so-called accretion disks, where two stars are in orbit about each other and any exchange of mass therefore possesses a substantial amount of angular momentum instilled by the binary orbital plane. In order for the material to accrete onto one of the stars, it must lose angular momentum (and radiate that energy away) on its path inwards —this leads to large radiative output that we can observe at many different wavelengths of light and which often changes dramatically with time.
The development of realistic accretion disk simulations and their output can be used to test various accretion disk models against the type of observed flux variability. As an example, above is a simplistic hydrodynamic simulation of a thin accretion disk embedded in a hot corona centered on a black hole. Here, we see an edge-on view of half the accretion disk, with a black hole residing at the origin. As the material in the disk evolves with time, we see evidence of Kelvin-Helmholtz instability (similar to wind causing waves across the surface of the ocean)— This kind of behavior is predicted to arise from the equations of hydrodynamics for disk-corona type systems (Shadmehri et al. 2010).
However, the situation becomes much more complicated in real systems: magnetic fields and radiative transfer are important physics that interact with the hydrodynamics and can lead to different behavior of the accretion flow. In addition to building more advanced simulations including these effects (often extremely time consuming and computationally expensive), we can develop methods of analysis for observational data — such as how the flux varies with time — in order to infer the instabilities that arise in accretion disks and compare with predictions from accretion disk simulations.
Classifying Light Curves
There is evidence that nonlinear and chaotic behavior exists in the light curves of X-ray binaries. What about for Active Galactic Nuclei (AGN)?
The light curves of AGN are canonically stochastic and difficult to model. Large ensembles of light curves of AGN, though spanning several years, often have few data points, are irregularly sampled and have large gaps. AGN can be identified by their stochastic behavior with this kind of data, as they are well-modeled by a damped random walk process (e.g. MacLeod et al. 2010; Baldassare et al. 2018), or similar (e.g. Moreno et al. 2019). However, correlations of the variability characteristics from these models with physical parameters, such as the black hole mass, are difficult to acquire. One solution to this problem is to obtain high cadence light curves of these elusive objects.
This Seyfert 1 galaxy was observed by the Kepler telescope over a few years. Although the flux over time appears to be stochastically driven, this source has an identified quasi-periodic oscillation (Smith et al. 2018). There are also traces of possible nonlinear behavior that we found using the method of recurrence analysis. Using the powerful recurrence plot from recurrence analysis, we can distinguish between stochastic and deterministic behavior. The power of higher cadence, and higher order modeling is critical for identifying variability features that trace with physical characteristics of black holes, such as mass or luminosity.
Chaos in the Cosmos!
The case of X-ray Binaries:
X-ray Binaries exhibit flux variability on multiple timescales. Furthermore, the variability is not strictly periodic. The well-studied black hole XRB, GRS 1915+105, has upwards of 14 classes of variability. In fact, Misra et al. 2004 computed the correlation dimension (a means to trace the presence of chaos, and related to the fractal dimension) of twelve of the temporal classes of GRS 1915+105 and determined that the underlying dynamical mechanism is a low-dimensional chaotic system for four of the classes, while three classes appeared stochastic and the remainders apparently random.
Potential chaotic variability on shorter timescales has also been detected for four other black hole XRB systems in addition to GRS 1915+105 using a nonlinear time series analysis technique called recurrence analysis (Sukova et al. 2016).
We recently detected long-term variability (on the order of hundreds of days) that exhibits nonlinear and chaotic behavior in the neutron star X-ray binary, 4U 1705-44 (image below). We compare the topological properties of a double-welled nonlinear oscillator (Duffing oscillator) to the timing evolution of 4U1705-44 embedded in a higher dimensional space, called the ‘phase space.’ We find a dominant unstable period of approximately 120 days in the light curve.
Phase space for astrophysical light curves:
In studies of nonlinear dynamics, the modeling of a dynamical system relies on the concept of phase space, which is the projection of the possible states of the system.
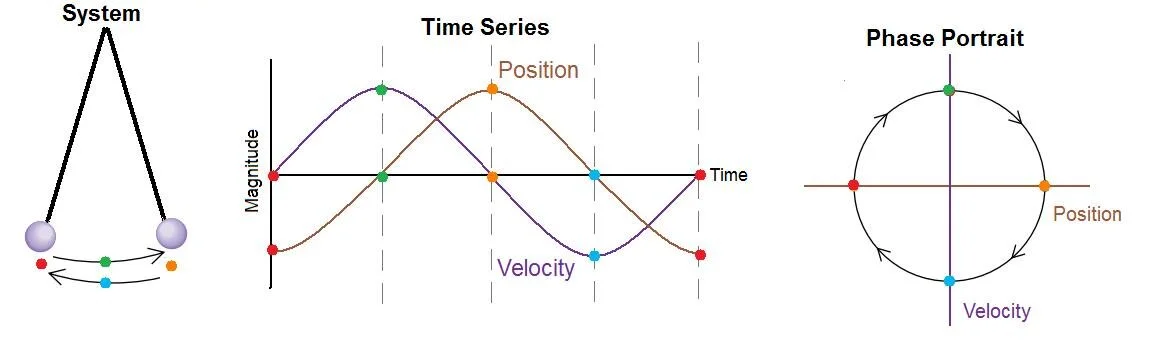
For example, think of a simple pendulum:
Highlighted are four moments in time identified by measurements of position and velocity. Plotting these values against each other traces out a circle in the phase portrait. The shape of the object in phase space (a circle) tells us there is only one possible trajectory, and thus only one future for the time series (or one solution to the equations of motion).
For the case of the Duffing Oscillator (chaotic!):
The phase portrait of the Duffing oscillator begins to trace out a more complicated shape than the simple circle of a simple pendulum. But, we can quantify the geometric structure of phase space through techniques from nonlinear dynamics and topology. We can then make comparisons between the Duffing oscillator’s phase space and that of 4U 1705-44 above —they are very similar! (Phillipson et al. 2018)
Recurrence Analysis
A recurrence plot (see the review by Marwan et al. 2007) is the graphical representation of a 2D matrix which contains all of the correlations in a time series. This is very similar to the linear autocorrelation function: when we compare each position in a time series to every other position in the time series, if two positions are ‘close’ to each other (i.e. the amplitudes are within some threshold of each other), then we input an entry of ‘1’ into the matrix, and ‘0’ otherwise. The location of the entry in the recurrence matrix corresponds to the two points in time. The difference between an autocorrelation function and the correlations that appear in a recurrence plot:
An autocorrelation function considers linear correlations in a scalar time series — it is more or less the summation of distances between two points in a time series, as a function of their time separation.
A recurrence plot considers correlations that are two positions in a time series that are near to each other in phase space. If we were to sum up all the non-zero entries along the diagonals starting with the main diagonal and working our way to the bottom right corner, we would get the equivalent to an autocorrelation function — the critical difference is the intermediary step of embedding the original time series in the higher dimensional space of phase space.
Here are some classical recurrence plots:
From left to right: 1) Gaussian white noise; 2) a sinusoidal signal (two sine waves of different periods added together); 3) the logistic map with a linearly increasing trend; and 4) the Duffing oscillator.
A black dot is an entry of ‘1’ in the recurrence matrix, and white space is an entry of ‘0’.
Randomness: appears as uniformly distributed, randomly placed black dots (e.g. white noise).
Periodicity: appears as diagonal lines and structures
Quasi-periodicity: repeating structures, checkerboard features
Non-stationarity: broad swathes of white, or fading regions towards the corners
Any scalar time series can be embedded in a higher dimensional phase space — one popular method of doing so is the Time Delay method.
The unique structures in the recurrence plot can be quantified — this is called ‘recurrence quantification analysis’ (as introduced by Zbilut and Webber Jr., 1992; Webber Jr. and Zbilut, 1994; Marwan et al. 2002) and is a means to distinguish different types of dynamical behavior (e.g. stochastic from periodic; randomness). An overview of these quantification schemes can be explored here.
Recurrence Plots of two Active Galactic Nuclei
Optical monitoring by the Kepler satellite over approximately 3 years of two Seyfert 1 galaxies show slightly different behavior as revealed in their recurrence plots. Left: KIC 9650712, which has a detected quasi-periodic oscillation of 44 days. Right: the canonical Zwicky 229-015 AGN, which has been well-modelled by damped random walk models.
Results of this analysis can be found in our paper here: Phillipson et al. 2020